3. Jason is doing his math homework. He has to find the square root of 10. He presses *square root sign*10 to his calculator and the screen displays 3.16227766. However, when 3.16227766 is multiplied by itself the answer is not 10. Explain.
- When 3.16227766 is multiplied by itself the answer is 9.999999999467538, it is not a perfect 10 because it is an estimate. It is estimated because if we want to get a perfect 10 there would be too many decimals.
10. Kai uses an entire can of paint on a square backdrop for the school play. The label on the can states that one can cover 27 squared metre of wall surface. Estimate the backdrop's side length, to one decimal place.
- First we have to find the square root in order to find one side of the square. *square root sign*27= 5.2 (The question says estimate to one decimal place so I estimated it and it's 5.2)

*Remember- The formula is s x s= a (area of a square)

- So 5.2 x 5.2= 27. 04 which is not a perfect square root to get 27 but it is an estimate which is pretty close to 27.
12. While shopping online, Ji Hun finds a square rug with an area of 11 squared metres. He need to know if it would fit in his 4 m x 5 m bedroom.
a. Estimate the side length of the rug, estimate to one decimal place.

b. Check your estimate with a calculator.
- 3.3 x 3.3 = 10.89 squared metres
c. Will the rug fit? Explain.
- Yes the rug will fit. Because if we calculate 0.20 (the area of the bedroom) x 10.89 (3.3 x 3.3 = 10.89- The rug) it would equal to 2.178 m which is the remaining metres of the bedroom after the rug has been placed.
PYTHAGORAS
1. Answer in a short paragraph and with diagrams
 - This equation mean the area of the square on the hypotenuse (the longest line in a right triangle) is equal to the sum of the areas of the squares of the other two sides(legs)— that is, a2 + b2 = c2.
- This equation mean the area of the square on the hypotenuse (the longest line in a right triangle) is equal to the sum of the areas of the squares of the other two sides(legs)— that is, a2 + b2 = c2.
2. Solve for the missing side length.
1. Answer in a short paragraph and with diagrams
 - This equation mean the area of the square on the hypotenuse (the longest line in a right triangle) is equal to the sum of the areas of the squares of the other two sides(legs)— that is, a2 + b2 = c2.
- This equation mean the area of the square on the hypotenuse (the longest line in a right triangle) is equal to the sum of the areas of the squares of the other two sides(legs)— that is, a2 + b2 = c2.EXAMPLE

So, I made a pythagoras problem here and it is asking for the length of the hypotenuse. In order to get that we need to use the formula a2 + b2 = c2.

So, I made a pythagoras problem here and it is asking for the length of the hypotenuse. In order to get that we need to use the formula a2 + b2 = c2.
- First, we need to get the area of leg a, it has an area of 10 cm. To get that we need to multiply 10 cm by itself. 10 cm x 10 cm = 100 squared centimetre (cm2)
- Secondly, we also need to find the area of leg b, it has an area of 15 cm. So, we again need to multiply it by itself. 15 cm x 15 cm = 225 squared centimetre (cm2)
- Third, we now need to add the two areas and we should be able to get the area of the hypotenuse or c. 100 cm2 + 225 cm2 = 325 cm2.
- Lastly, we need to find the square root of 325 cm2 because it doesn't fit the 10 cm and 15 cm side length of the two legs. 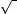 325 = 18.02 cm
325 = 18.02 cm
- There it is the hypotenuse of this right triangle is measured 18.02 cm
2. Solve for the missing side length.
- Use the formula a2 + b2 = c2. Lets name 5 cm a, 12 cm b, and the hypotenuse c.
- Firstly, we need to find the area of 12 cm. 12 cm x 12 cm = 144 squared centimetre (cm2)
- Secondly, we need to find the area of 5 cm. 5 cm x 5 cm = 25 squared centimetre (cm2)
- Thirdly, we need to add the two areas of the legs. 25 cm2 + 144 cm2 = 169 cm2
- Lastly, we need to find the square root of 169 cm2 to fit the side length 5 cm, and 12 cm.
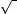 169= 13 cm. There it is, the missing side length is 13 cm
169= 13 cm. There it is, the missing side length is 13 cm
- Thirdly, we need to add the two areas of the legs. 25 cm2 + 144 cm2 = 169 cm2
- Lastly, we need to find the square root of 169 cm2 to fit the side length 5 cm, and 12 cm.
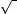 169= 13 cm. There it is, the missing side length is 13 cm
169= 13 cm. There it is, the missing side length is 13 cm3. Is this a right triangle? Prove it!!!

- To see we need to use the formula a2 + b2 = c2. If the area of the 2 legs doesn't add up to the area of c then it is not a right triangle.
- First, we need to find the area of 6 cm. 6 cm x 6 cm = 36 squared centimetres cm2
- Second, we need to find the area of 8. 8 cm x 8 cm = 64 squared centimetres cm2
- Third, we need to add the area of the two legs. 36 cm2 + 64 cm2 = 100 cm2
- Lastly, we need to find the square root of 100.
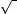 100= 10 cm
100= 10 cm- The sum of the two areas of the legs is not 11 cm which is depicted in the right triangle so this means that this is not a right triangle.
*Video-
*Message- Thanks for viewing my post and please leave a comment. Bye :))

AMAZING JOB Carlo! Your answers to your questions were very well said also your pictures were flawless! The video and link were also very helpful to me so I think they will be helpful to others as well. One suggestion I have, to make your scribepost even better is that you could've added some color to make it stand out more but otherwise great job and keep up the hard work.
ReplyDeleteHey Carlo! You did a well built scribe here. I like how you included LOTS of information and you supported it with your pictures. Also, the video and the link were very helpful. Although you didn't add some colours, you still made some important words bold. This scribe really helps me. Good job Carlo! Keep up the good work!
ReplyDeleteHey there Carlor! Great post you got here! I loved how you added TONS of pictures, it made me understand this! The video was outstandingly helpful! But what Alyshia and Joshua said add more color to make it really pop! But overall GREAT job! Keep it up!
ReplyDeleteGood job Carlo! your pictures and answers were clear and easy to read. your link and video was also helpful, but one thing that you should add next time is a little bit more color, but other than that great job again!
ReplyDelete